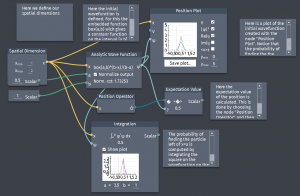
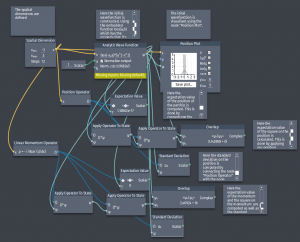
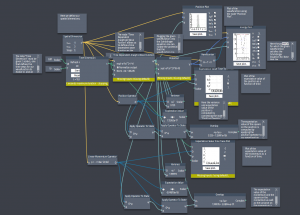
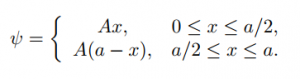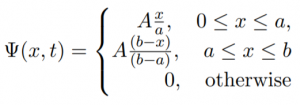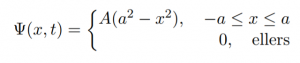Examples of interesting systems

In these pages you will find interesting examples of quantum systems solved in Quatomic Composer. The examples are all phrased as questions. You can try to solve these questions yourself, or download solutions.

The examples mainly originate from exercises from D. J. Griffiths "Introduction to Quantum Mechanics" (4. edition), but there is not necessarily a direct corrosponcences between the examples and the exercisises in the book.

Infinite square well.

A particle in the infinite square well has initial wave function:

Expectation values in the infinite square well.

Find $\langle x \rangle$, $\langle p \rangle$, $\langle x^2 \rangle$, $\langle p^2 \rangle$, $\sigma_x$ and $\sigma_p$ for a particle in the $n$'th stationary state of the infinite square well.

Linear combinations in the infinite square well.

A particle in the infinite square well has wave function:

$\Psi(x,o)=A\left[\psi_{1}(x)+\psi_{2}(x)\right]$

Perturbation in the infinite square well.

Suppose we place a delta-function bump in the middle of a infinite square well of width $a$, then we have the perturbation:

$H'=\alpha\delta(x-\frac{a}{2})$

Phaseshift.

A particle has  an initial wave function, which is an equal mixture of two eigenstates:

$\Psi(x,0)=A[\psi_{1}(x)+\psi_{2}(x)]$

Eigenstates of the harmonic oscillator.

In this problem we are studying the harmonic oscillator, i.e. the potential $V(x)=\frac{1}{2}m\omega^2 x^2$. 

Linear combinations in the harmonic oscillator.

A particle in the harmonic oscillator has initial wave function:

$\Psi(x,0)=A[3\psi_{0}(x)+4\psi_{1}(x)]$

Expectation values in the harmonic oscillator. 

Find $\langle x \rangle$, $\langle x^2 \rangle$, $\langle p \rangle$, $\langle p^2 \rangle$ and $\langle T \rangle$ for the $n$'th stationary state of the harmonic oscillator.

Half harmonic oscillator.

Find the allowed energies for the half harmonic oscillator. 

A free particle. 

A free particle has initial wave function:

$\Psi(x,0)=A\exp(-a|x|)$

where  $A$ and $a$ are positive constants. 

Particle with a given wave function.

At the time $t=0$ a particle has wave function:

where $a$,$b$ and $A$ are constants. 

Expectation values for a particle with in a given state. 

A particle has initial wave function:

Time-dependent wave function. 

A particle with mass $m$ is in the state:

$\Psi(x,t)=A\exp{-a\left[\left(\frac{mx^2}{\hbar}\right)+it\right]}$

Where $A$ and $a$ are positive, real constants.

Double-delta-function potential. 

Consider the double delta-function potential

$ V(x)=-\alpha\left[\delta(x+a)+\delta(x-a)\right]$

where $\alpha$ and $a$ are positive constants.

The delta-function potential approximated with a finite square well. 

This assignment studies how we can approximate the delta-function potential with a finite square well.