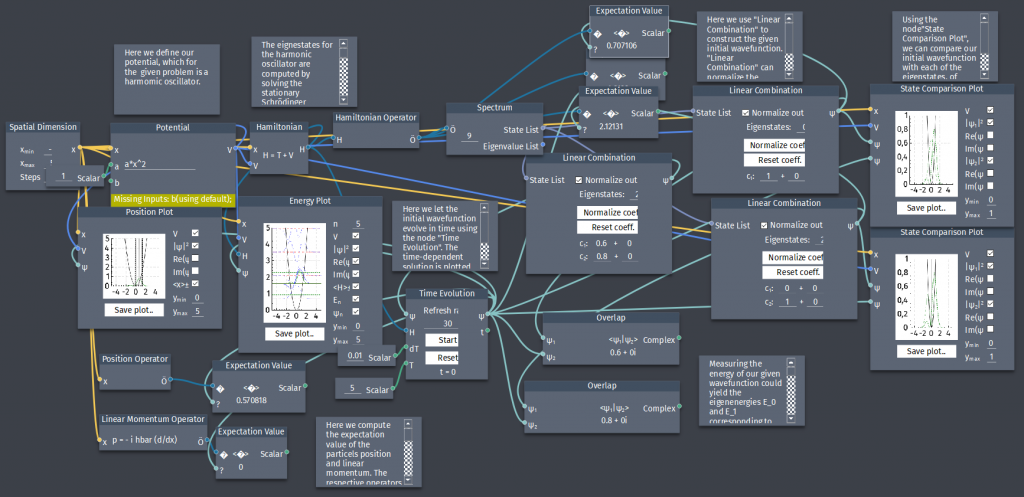
Linear combinations in the harmonic oscillator
A particle in the harmonic oscillator has initial wave function:
$\Psi(x,0)=A[3\psi_{0}(x)+4\psi_{1}(x)]$
a) Determine $A$ to normalize $\Psi(x,0)$.
b) Construct the time-dependent state $\Psi(x,t)$ and observe the overlap $\langle \Psi(x,t)|\Psi_{0}(x,0)\rangle$ and $\langle \Psi(x,t)|\Psi_{1}(x,0) \rangle$.
c) Compute $\langle x \rangle$ and $\langle p \rangle$.
d) Compute the energy of $\Psi(x,t)$.