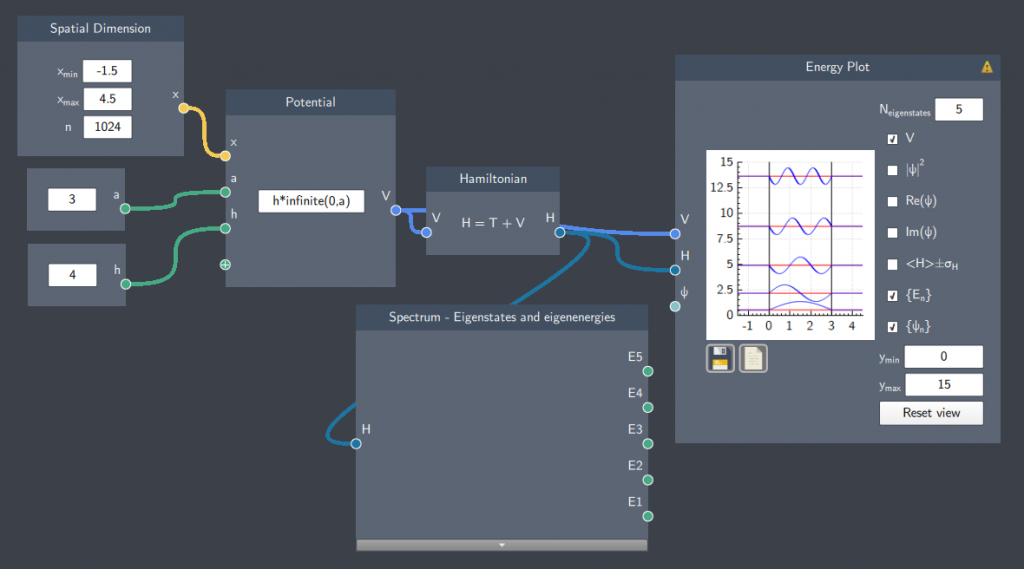
Hamiltonian

Description

The Hamiltonian node defines the total energy of the system. It is the first building block to get the energy spectrum of a system.

Input

The node has the following input: 

• Potential (V): As the Hamiltonian is the sum of the potential and kinetic energy of a system, it requires a potential function defined in the Potential node as its input.

Content

The content in the node shows what is being calculated. It is the sum of the kinetic and potential energy. The kinetic part $T = \frac{-\hbar^2}{2m} \frac{\partial^2}{\partial x^2}$ is calculated from the spatial dimension $x$, while the Potential ($V$) is taken from the Potential node.

 Output

After the input is provided, the node gives the following output:

• Hamiltonian (H): The Hamiltonian of the defined system. 

Example

In the example below, the Hamiltonan of an infinite well potential is calculated to plot the eigenstates and calculate the spectrum of eigenenergies.