Time Evolution

Description

The Time Evolution  node is one of the building blocks to observe the dynamics of a system over time. It is inserted inside a time loop which evolves an initial state by solving the time-dependent Schrödinger equation (TDSE).

Inputs

The node has the following inputs: 

• Initial State ($\psi_{0}$): An initial state is required as an input which is evolved over time. 
• Hamiltonian (H(t)): An input from a Hamiltonian node which is evolved over time.
• Time step (dt): A scalar quantity that defines the rate of change of time in the evolution of the system.

Content 

At each time step, it will numerically solve the TDSE and update the initial state to give the time-evolved state. 

 Output

After the inputs are provided, the node gives the following output:

• Time-evolved state ($\psi_{t}$): The state evolved after each time step.

Example

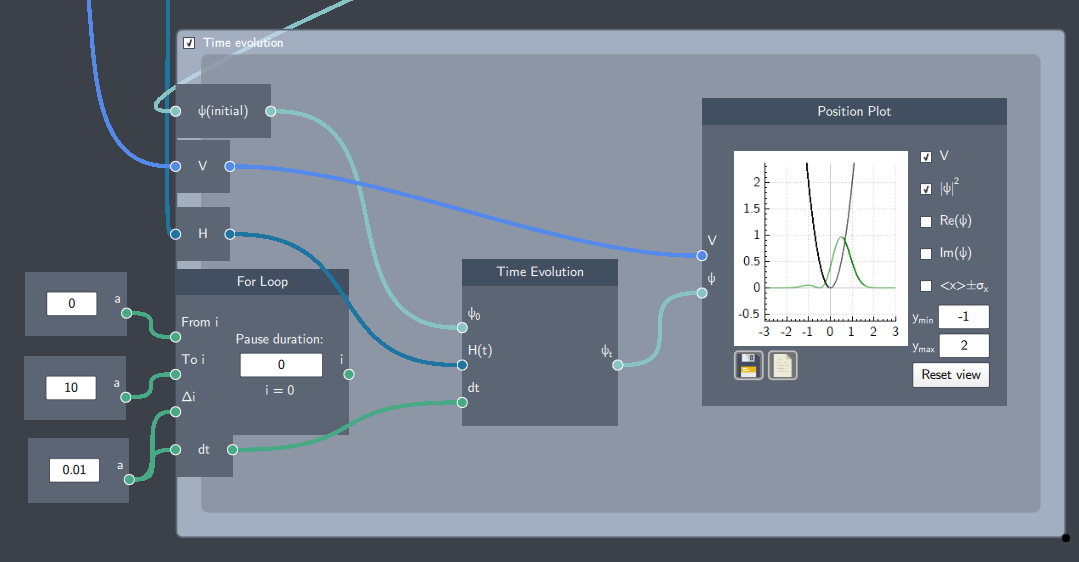
In the example below, the set-up shows the time evolution of a linear superposition state in a harmonic oscillator.  The Time Evolution node is inserted inside the time loop which evolves the superposition state.

The time dynamics of the system can be seen in the plot when the simulation is running. If the Potential and Hamiltonian is also time dependent, they must be placed inside the For Loop as well. The output $i$ from the For Loop boundary node can be used as input to these as the time variable.