State Analysis

The State Analysis category consists of 7 nodes that relate to the analysis of a state/wave function and operators

Overlap
Calculate the overlap $\langle \psi_1 | \psi_2 \rangle$ between two states

Expectation Value

Calculate the expectation value of any operator with regard to an arbitrary state

Squared Expectation Value

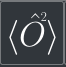
Calculate the squared expectation value of any operator 

Standard Deviation
Calculate the standard deviation $\sigma = \sqrt{\langle\hat{O}^2 \rangle - \langle\hat{O} \rangle ^2}$ of an operator $\hat{O}$

Variance
Calculate the variance $\sigma^2= \langle \hat{O}^2 \rangle- \langle \hat{O} \rangle ^2$ of an operator $\hat{O}$

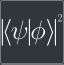
Fidelity
Calculate the fidelity $F = |\langle \psi | \phi \rangle |^2$ between two states

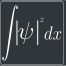
Integration
Calculate the integral of the probability density of a state $\int_a^b |\psi|^2 dx$