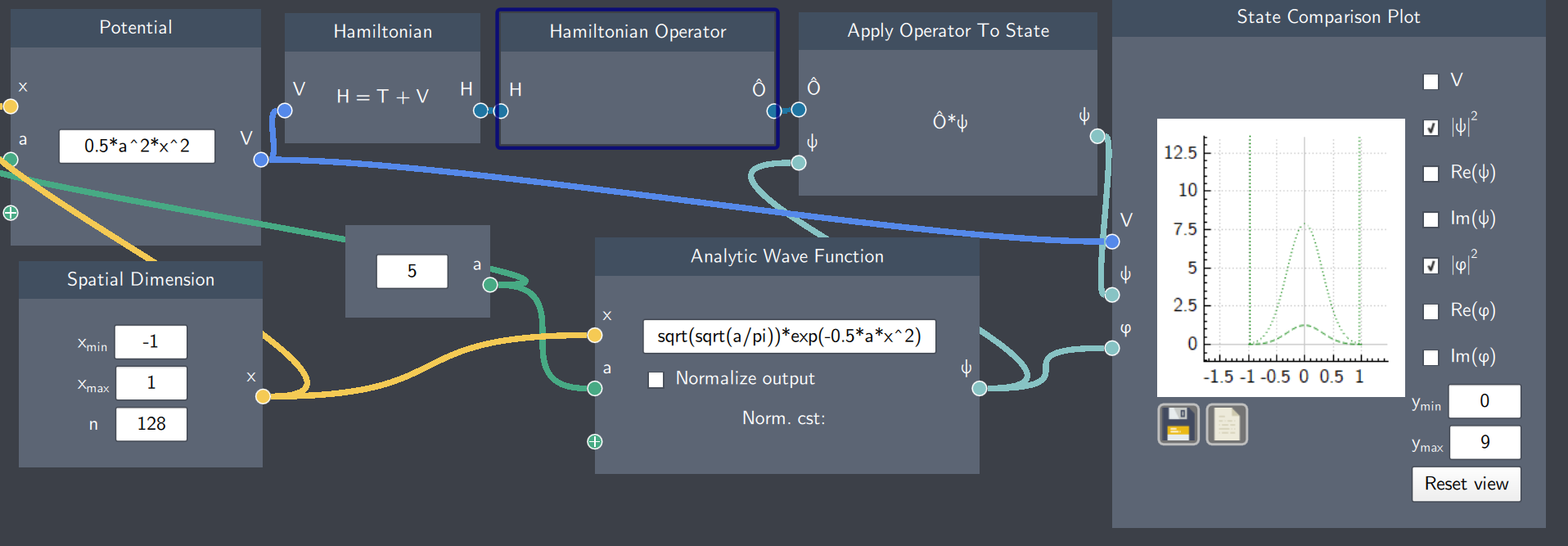
Hamiltonian Operator

Description

The Hamiltonian Operator is the quantum mechanical operator that changes the Hamitonian to an operator. 

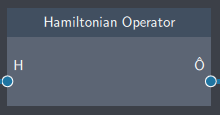
Input

• Hamiltionian (H): It inputs the Hamiltonian node

Content 

The Hamiltonian Operator is the sum of the kinetic ($\hat{T}$) and potential ($\hat{V}$) operators. The kinetic operator is a linear momentum-based operator which yields kinetic energy. The potential operator is a position-based operator, which yields the potential energy. In this node, both these operators are combined to give the Hamiltonian operator yielding the total energy of the system. 

Output

• Hamiltonian Operator : The Hamiltonian Operator $\hat{H}$.

Example 

In the example below, the Hamiltonian Operator node inputs the Hamiltonian of a harmonic oscillator and applies it to a Gaussian function to give a new function. The magnitudes of both the Gaussian and the resulting function after operator application are shown on the plot. Note that the original function has been scaled by the energy of the state, as expected due to the fact that $\hat{H}\psi = E\psi$.