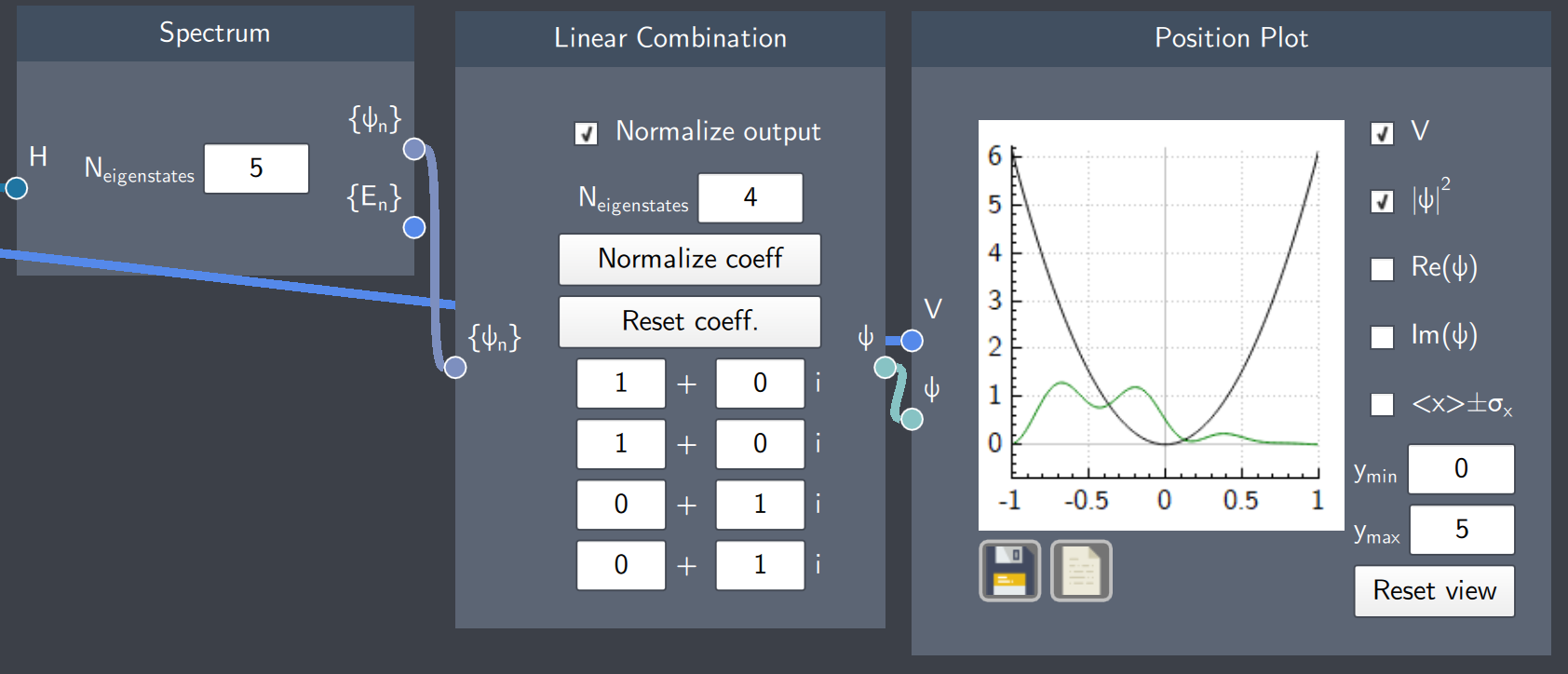
Linear Combination

 Description

This node creates a linear combination of eigenstates. You can create a linear combination of states by entering values for the coefficients. For example, for the coefficients $c_{0}$ and $c_{1}$ in the linear combination $\psi(x) = {\sqrt\frac{1}{2}(c_\mathrm{0}\psi_0(x) + c_\mathrm{1}\psi_1(x))}$, they are entered in the text-fields as shown in the annotated screenshot below.

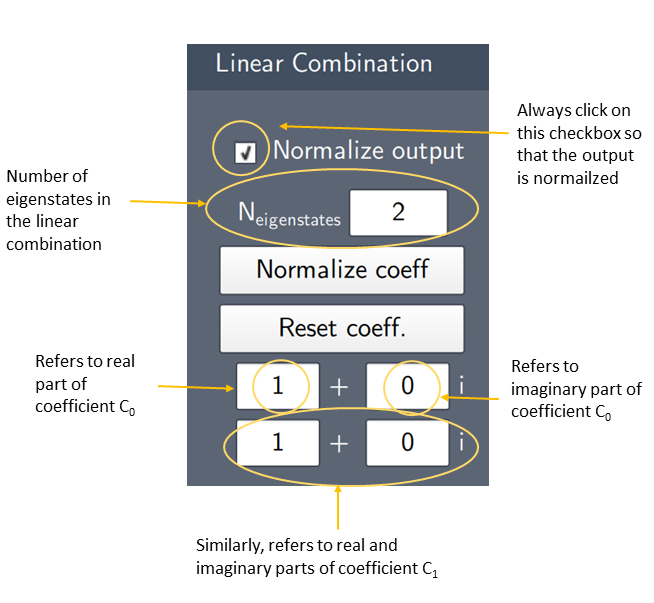
Input

The node has the following input:

• Spectrum of eigenstates ($\{ \psi_n \} $): The list of eigenstates of the system (defined by the Hamiltonian) calculated in the Spectrum node.

Content

In this node, there are 5 essential content fields. The first is the text-field $N_{eigenstates}$ that defines the number of eigenstates in the linear combination. Second, there is a collection of text-fields that define the coefficients of the linear combination. The remaining content fields are: a checkbox for numerically normalizing the resulting state, a button for directly normalizing the user-input coefficients, and a button for resetting the coefficients to $c_0 = 1, c_n = 0$. The node shows a warning if $N_{eigenstates}$ exceeds the number of eigenstates calculated by the Spectrum node.

Output

• State ($\psi$):  The result of the linear combination of eigenstates. This node will output a superposition state if there is a combination of minimum two eigenstates.

Example

In the example below, the linear combination of four eigenstates of a harmonic oscillator is calculated. As $N_{eigenstates}$ is "4" in the Linear Combination node, the coefficients for each eigenstate is entered in the text-fields below. The left column gives the real part of the coefficients and the right column gives the imaginary part of the coefficients. The output is normalized by checking the ''Normalize output''' box. The superposition state is shown on the plot.