GPE Time Evolution
Description
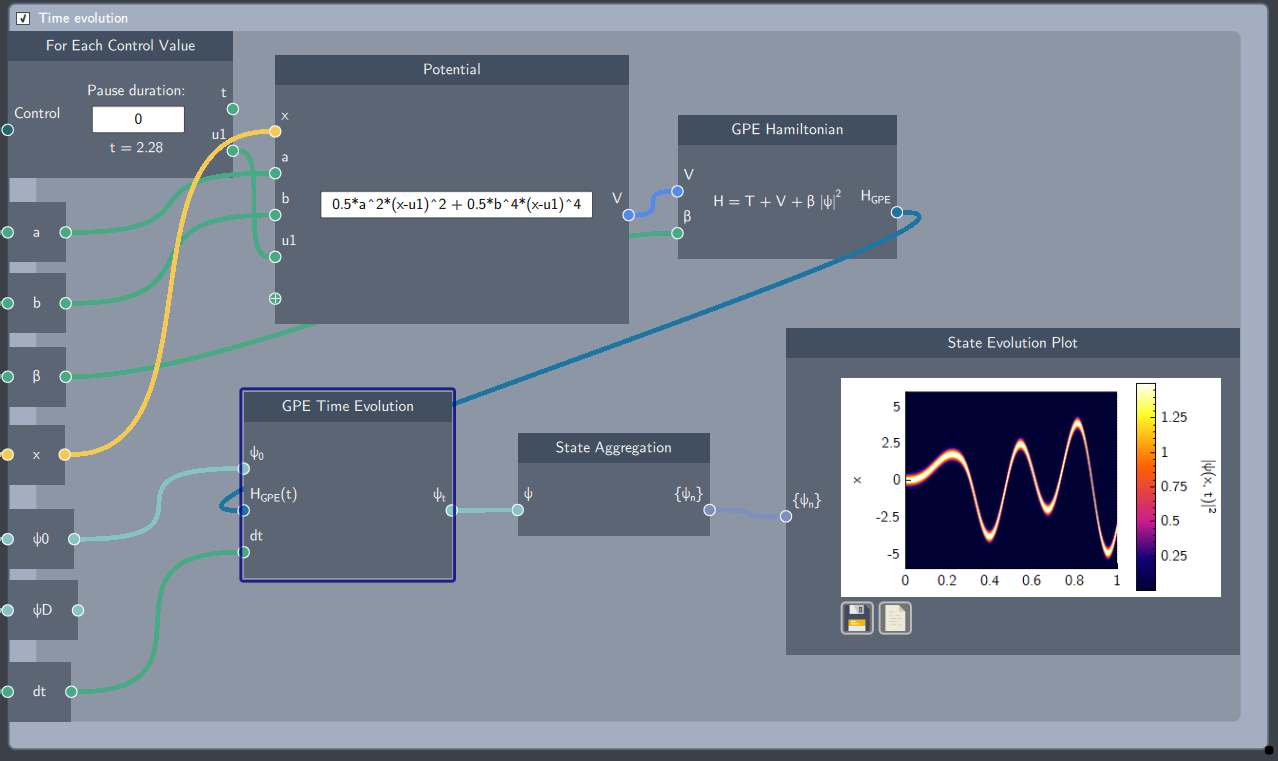
The GPE Time Evolution node is one of the building blocks to observe the dynamics of a system modelled by the Gross-Pitaevskii Equation (GPE) over time. It is inserted inside a time loop which evolves an initial state by solving the time-dependent GPE.
See also https://www.quatomic.com/composer/reference/quantum-basics/time-evolution-2/

Inputs
The node has the following inputs:
- Initial State ($\psi_{0}$): An initial state is required as an input which is evolved over time.
- GPE Hamiltonian ($H_{GPE}(t)$): It inputs the GPE Hamiltonian node which is evolved over time.
- Time step (dt): A scalar quantity that defines the rate of change of time in the evolution of the system.
Content
At each time step, this node will numerically solve the time-dependent GPE and update the initial state to give the time-evolved state.
Output
- Time-evolved state ($\psi_{t}$): The state evolved after each time step
Example
In the example below, an anharmonic potential is controlled over time which dynamically evolves an initial state modeled by the time-dependent GPE. The GPE Time Evolution node should always be inside a For Loop or For each Control Value node.