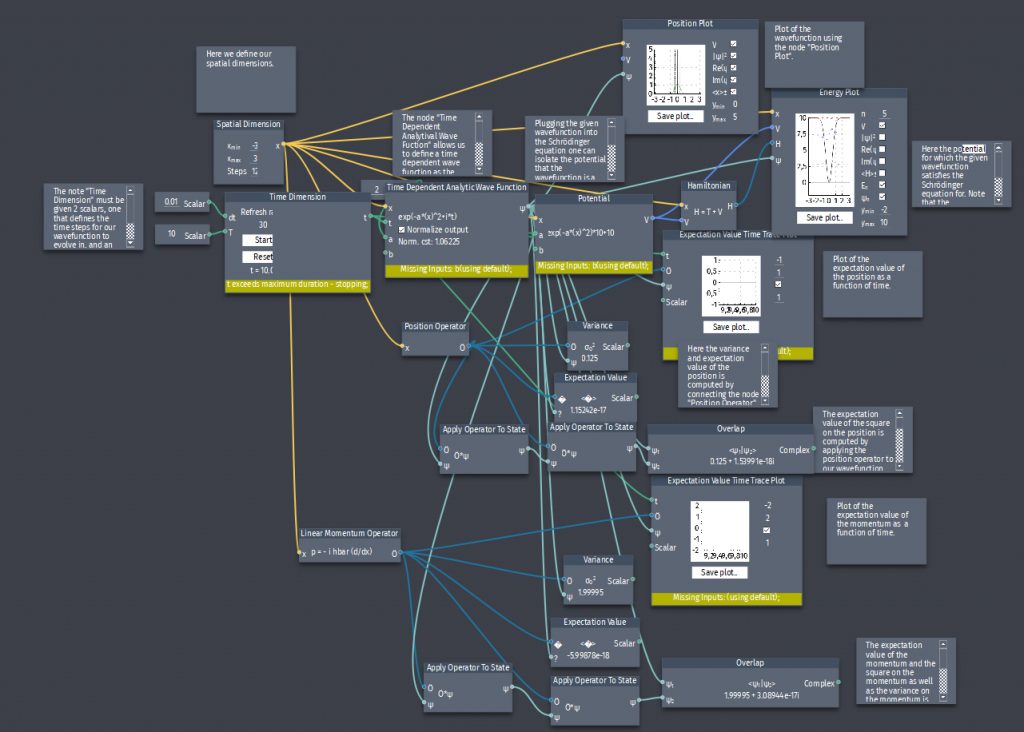
Time-dependent wave function
A particle with mass $m$ is in the state:
$\Psi(x,t)=A\exp{-a\left[\left(\frac{mx^2}{\hbar}\right)+it\right]}$
where $A$ and $a$ are positive real constants.
a) Find $A$.
b) For what potential energy function $V(x)$ does $\Psi$ satisfy the Schrödinger equation? This must be calculated analytically, but use composer to test that $\Psi$ is a solution to the Schrödinger equation for your calculated potential.
c) Calculate the expectation values of $x,x^2,p$ and $p^2$.
d) Calculate the standard deviation of the position $\sigma_x$ and the momentum $\sigma_p$.