Phaseshift
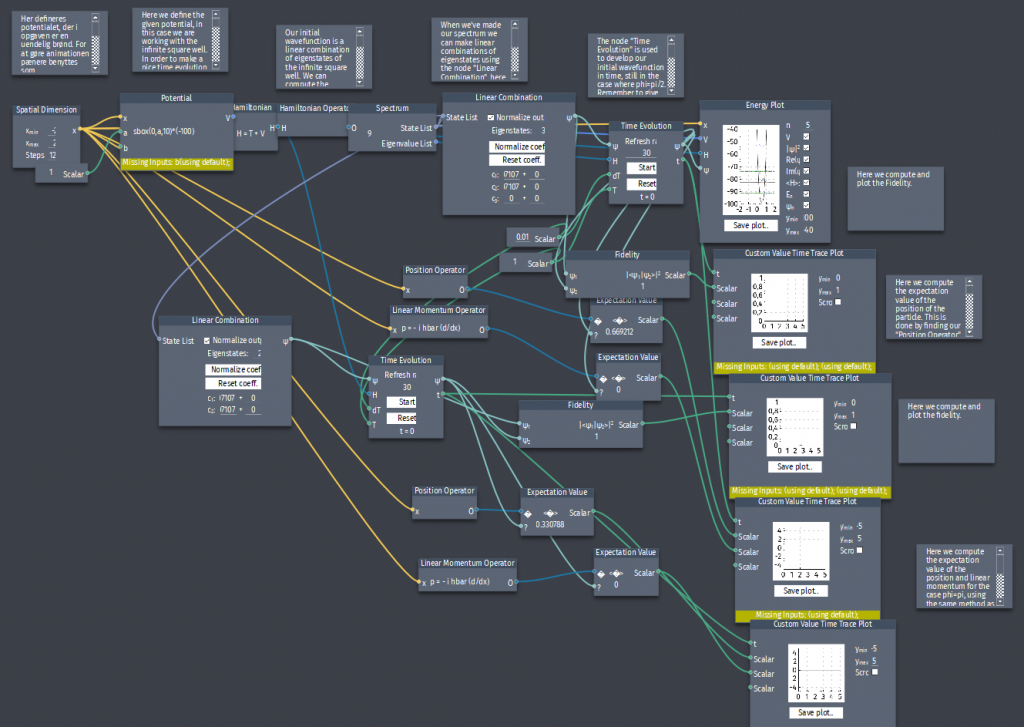
A particle i the infinite square well has an initial state which is an equal mixture of 2 states:
$\Psi(x,0)=A[\psi_{1}(x)+\psi_{2}(x)]$
a) Normalize $\Psi(x,0)$ and compute the fidelity $|\langle \Psi(x,t=0) |\Psi(x,t)\rangle|^2$
b) Compute $\langle x \rangle$,$\langle p \rangle$.
c) Repeat for the state $A[\psi_{1}(x)-\psi_{2}(x)]$, i.e. making a phaseshift.
d) Plot the expectation value of the position and the momentum and the fidelity and compare the two states. How are they alike, and how do they differ?