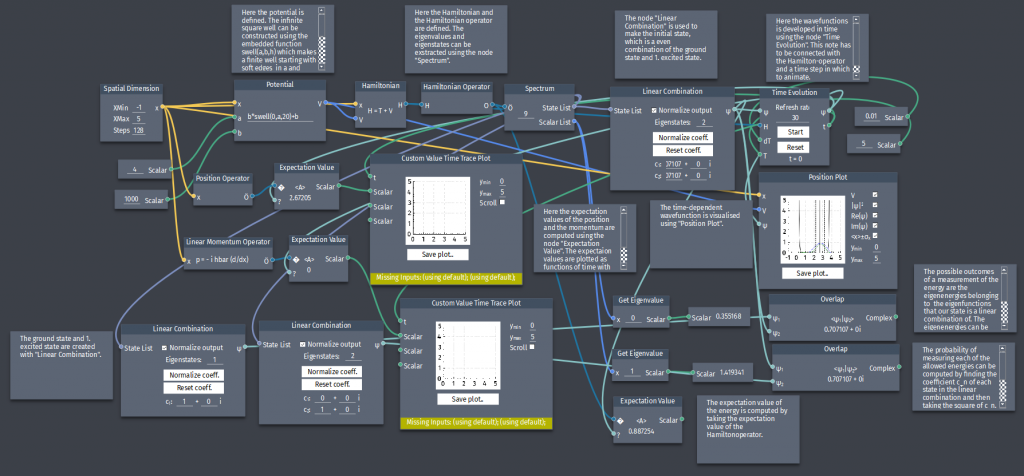
Linear combinations in the inifinite square well
En partikel i den uendelige brønd har startbølgefunktion:
$\Psi(x,0)=A\left[\psi_{1}(x)+\psi_{2}(x)\right]$
a) Normalize $\Psi(x,0)$.
b) Find $\Psi(x,t)$ and $|\Psi(x,t)|^2$.
c) Compute the expectation value of $x$. Notice that it oscillates in time and plot $\langle x \rangle$ as a function of $t$.
d) Compute the expectation value of $p$.
e) If you measured the energy of this particle, what values might you get and what is the probability of getting each of them? Find the expectation value of the energy and compare it with the eigenenergies $E_1$ and $E_2$.